Les trous noirs

4 Les différents types de trous noirs théoriques

A) Le trou noir de Schwarzschild

Le trou noir de Schwarzschild est le premier trou noir théorique découvert par un physicien en réponse aux équations qu’avait mis en œuvre Einstein lors de sa théorie de la relativité générale en 1915. En 1916, Karl Schwarzschild trouve des solutions aux équations de Einstein pour former un trou pour cela Schwarzschild démontra de façon assez mathématique l’existence du rayon à partir duquel aucun objet ou bien particule ne peut s’échapper d’un trou noir celui-ci sera appelé rayon de Schwarzschild. Nous allons tout d’abord voir la démonstration la plus difficile mathématiquement, pour cela, il nous faut la métrique de Schwarzschild qui est démontrée de façon très mathématique et relativement compliqué le résultat est le suivant :

Cette équation est sous la forme d’équation en système de coordonnées sphériques car les principaux objets étudiés ont une symétrie sphérique. On peut facilement comprendre que pour que l’objet en question soit une singularité il faut que l’équation suivante soit vérifiée :

Pour trouver, le rayon pour lequel aucun objet ne pourra sortir de cette singularité il faut résoudre cette équation et le résultat obtenu sera appelé Rayon de Schwarzschild (Rs) :

Pour trouver ce résultat, il y a une autre méthode qui n’utilise pas la métrique de Schwarzschild mais la vitesse de libération, cette vitesse est égale à la vitesse nécessaire à un objet pour s’échapper du champ gravitationnel d’un astre. Pour cela on doit égaliser la force centripète (qui est du à la forme de l’astre en question) et la force de gravitation, la démonstration est la suivante :

Ce qui donne après simplification une vitesse orbitale qui est la suivante :

Or a la vitesse de libération qui est égale à la vitesse orbitale multipliée par √2, ce qui donne :

Pour trouver le rayon pour lequel aucun objet ne peut s’échapper même à la vitesse de la lumière (ce qui est impossible car aucun objet en peut atteindre voire dépasser la célérité de la lumière), on doit donner une valeur à v₁ qui doit être égale à c, d’où l’équation et le résultat du rayon de Schwarzschild que l’on trouve est le suivant :

D'où:

On retrouve donc le résultat trouver précédemment dans la partie de la métrique de Schwarzschild. Ce rayon de Schwarzschild est en fait utilisé pour mesurer tous les rayons des trous noirs qu’ils soient de Schwarzschild ou bien de Kerr ou de Reissner-Nordström.

Nous allons passer maintenant au trou noir de Schwarzschild proprement dit, ce trou noir est en fait déduit de la métrique de Schwarzschild qui est fait pour les objets sphériques statiques et non en rotation( ce qui implique que le moment angulaire . Le trou noir de Schwarzschild est un trou noir non chargé ce qui est une des différence avec les autres types théoriques de trou noir.

Maintenant, pour décrire vraiment, le trou noir de Schwarzschild, je propose de faire le voyage d’un observateur (celui-ci peut aller à la vitesse de la lumière ce qui est impossible dans la réalité) qui irait vers un trou noir de Schwarzschild. En s’approchant de celui-ci sera confronté à des forces de marées (force générée par la différence de gravitation entre deux points qui sont à une distance différente l’astre principale) qui sont très intenses. Ensuite si on observe un objet se rapprochant du trou noir, on verra la lumière que l’objet émet qui se décalera dans les couleurs à grande longueur d’ondes c’est le redshift gravitationnel (que l’on montrera plus tard). De plus, plus on se rapproche du trou noir plus le temps se ralentira (du à la relativité), et on observera donc jamais l’objet traverser l’horizon du trou noir. En continuant son voyage, l’observateur va rencontrer la sphère de photons qui se trouve à environ 1,5R_S , on appelle cette sphère la sphère de photons car pour se mettre en orbite autour d’un objet il faut une vitesse de satellisation qui est égale à la célérité de la lumière pour un trou noir et les seules particules qui peuvent atteindre cette vitesse est bien entendue les photons qui sont les particules qui composent la lumière. Cette limite est immatérielle. Après cette sphère de photons on trouve une limite appelé horizon qui se trouve à une distance de la singularité égale au rayon de Schwarzschild après cette limite, on ne peut plus revenir en arrière, de plus la vitesse de libération après cette limite est plus grande que la célérité de la lumière donc c le début du trou noir. Ensuite on trouve la singularité (dont la définition scientifique est la suivante : volume infiniment petit où toutes les grandeurs (température, densité, courbure d’espace) deviennent infiniment grandes), qui est en fait le reste de l’étoile qui s’est effondrer selon la physique relativiste la densité de la singularité est infinie alors que sa taille est nulle alors qu’avec la mécanique quantique on trouverait que sa taille serait égale à 10^-35 m .

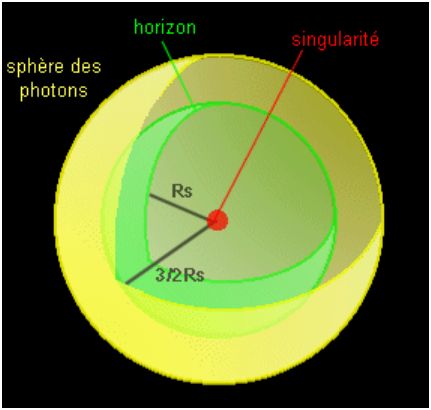-> Structure du trou noir de Schwarzschild

2. Le trou de Reissner – Nordström

Le trou noir de Reissner – Nordström est en fait la solution aux équations de la relativité générale de Einstein lorsqu’il y a présence de charges électriques. En effet, le résultat de la métrique de Reissner – Nordström (solutions des équations d’Einstein) est un trou noir de masse M, de charges non nulles Q et de moment angulaire nul d’où la formation de celui-ci n’est pas du à un effondrement d’une étoile en rotation. Ce résultat eut été trouvé en 1918 soit deux ans après le travail de Schwarzschild et trois ans après la publication des équations d’Einstein. Pour trouver ce résultat Hans Reissne r et Gunnar Nordström ont élargie la métrique de Schwarzschild à un objet chargé électriquement ce qui instaure alors un champs électrique et magnétique. La métrique trouvée est la suivante :

Ce résultat à lieu avec les unités géométriques et quand on prend la célérité de la lumière et la constante de gravitation de Newton égale à 1, c=G=1, sinon la métrique de Reissner et de Nordström est la suivante :

Où la partie angulaire est définit comme cela :

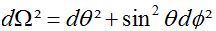
Avec cette métrique on trouve un potentiel électromagnétique (du à la charge différente de zéro) celui-ci a les coordonnées suivantes :

Pour les trous noirs chargés, il y a deux types bien différents, en effet, si on a la valeur absolue de la charge qui est inférieure voire très inférieure à la masse qui vérifie donc l’équation suivante : |Q| < M mais surtout |Q| = M. Si cette équation est vérifiée alors on n’est plus dans le cas d’un trou noir de Reissner – Nordström mais dans le cas d’un trou noir de Schwarzschild car la charge est alors considérée comme nulle. La démonstration des deux rayons solutions de l’équation ( deux car l’équation est un polynôme de deuxième degré) est la suivante pour trouver les rayons il faut que le coefficient suivant

soit égale à zéro d’où la démonstration suivante :

On calcul le discriminent de cette équation :

Ce qui permet de trouver deux solutions appelées r₊ et r_-

Si on reprend le système de coordonnées très simple qui induit que G=c=1 celui que l’on a utilisé au début on trouve si on reprend les deux équations précédentes :

On vient de trouver deux solutions, qui ont des significations dans le trou noir de Reissner - Nordström ce que nous allons voir maintenant avec le schéma suivant et ses explications:

-> Trou noir de Reissner – Nordström

Le trou noir de Reissner – Nordström est un peu comme le trou noir de Schwarzschild en effet le profil à peu près semblable en effet le trou noir de Schwarzschild est composé d’une couche de photon qui est ensuite suivie par une sphère qui est l’horizon où toute matière qui est rentrée dedans ne peut plus partir alors que dans le trou noir de Reissner – Nordström on trouve deux horizons qui proviennent des deux solutions de la métrique de Reissner – Nordström. En effet, à partir de la première ligne d’horizon appelée horizon extérieur, on trouve la gravité qui est encore plus grand que la force électromagnétique alors que dès que l’on passe la ligne d’horizon interne (qui correspond à la deuxième solution) on trouve alors que la force électromagnétique qui est plus grande que la gravité qui a pour conséquence que toutes les charges attirées ne peuvent plus s’échapper à cause des deux forces.

3. Le trou noir de Kerr

Le trou noir de Kerr qui a été découvert par Roy Kerr en 1963, ce trou noir peut en fait être matérialisé par une expérience faite en laboratoire si on met dans un bêcher d’eau un barreau aimanté, ce même bêcher sur un agitateur magnétique alors si celui-ci est mis en position de rotation maximale on peut observer un conne d’air au dessus du barreau ce qui peut représenter le trou noir de Kerr. Cela est du à la rotation de celui-ci. Pour trouver les paramètre d’un trou noir de Kerr il faut utiliser la métrique Kerr, celle-ci est la suivante pour un trou noir de moment angulaire est égale à J et  de masse M :

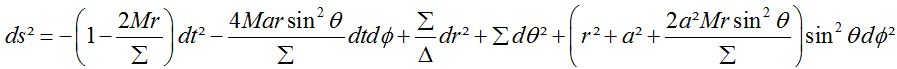
où , et avec , de plus pour ne pas alourdir l’écriture on a pris c=G=1

D’après la métrique de Kerr on peut trouver le rayon de ergosphère et les deux solutions pour le rayon de l’horizon. Pour trouver le rayon de l’ergosphère, il suffit que le facteur devant dt² soit égal à 0 :

On cherche le discriminent de cette équation :

Ce qui donne une solution à l’équation :

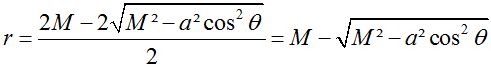
Si on met le résultat selon les variables connues comme le rayon de Schwarzschild, de la constante de gravitation de Newton, de la Masse du trou noir et du moment angulaire on a le résultat suivant :

On trouve ce résultat grâce aux relations suivantes : et .
Ensuite grâce à la relation de la métrique de Kerr, on peut aussi trouver les deux rayons de l’horizon en effet pour cela il faut poser ce qui donne la démonstration suivante tout d’abord on cherche le discriminent de cette équation (que l’on appellera &OMEGA par soucis de lisibilité) :

Puis, on trouve les deux solutions suivantes :

et

Ce qui donne avec les mêmes variables et les mêmes relations que cités précédemment :

et

-> Croquis à l’approche d’un trou noir de Kerr

Maintenant, voyageons virtuellement près de notre trou noir de Kerr, quand nous arrivons près de celui-ci nous rencontrons tout d’abord, une sphère de photons contrarotative c’est à dire une sphère de photons qui tourne autour du trou noir dans le sens opposés du sens de rotation de celui. Après cette sphère de photons contrarotative, on trouve une sphère de photons corotative, cela veut en fait dire que cette sphère de photons tourne dans le même sens que le trou noir autour de son axe de rotation. Ainsi, avec ces deux sphères de photons qui tournent l’une avec le sens contraire à l’autre, on peut se dire et cela est la vérité quand le trou noir tourne autour de son axe avec une très grande vitesse ,que les deux sphères s’éloignent l’une de l’autre.

-> Le trou noir de Kerr

Maintenant, nous allons nous rapprocher du trou noir en passant les deux sphères de photons, on arrive donc à la limite statique ce qui correspond au rayon que l’on a trouvé, plus tot dans ce même dossier. Dans l’ergosphère c'est-à-dire entre la limite statique et l’horizon extérieur, on trouve l ’ergosphère, dans celle-ci on n peut pas rester immobile du fait de la rotation du trou noir et de la rotation de l’espace temps autour de ce trou noir. Ensuite on trouve, le deux lignes d’horizon, qui ont le même rôle que dans le trou noir de Reissner – Nordström, ou bien de Schwarzschild, en effet l’horizon a pour rôle de permuter l’espace en temps et l’inverse et comme il y a deux permutation on peut donc trouver que la singularité qui se trouve ensuite est de type temporelle. Ce type de trou noir théorique est le plus probable dans la réalité en effet car lors de l’effondrement d’une étoile il y a de grande c chance que celle-ci tourne sur elle-même.

Tous les produits, logos et images cités dans ces pages sont la propriété de leurs marques respectives.
Site configuré sous le navigateur Mozilla Firefox - Résolution 1280*1024.
© Astronomie en Folie 2008-2011 - Créé par Kévin